Pythagoras merupakan salah satu rumus terkenal yang ada di dalam ilmu matematika. Umumnya teori rumus teorema pythagoras dipelajari pada kelas 8 SMP. Tetapi tak jarang dasarnya sudah diberikan sejak kelas 4 Sekolah Dasar.
Rumus Pythagoras ini sebenarnya adalah cara untuk menghitung sisi dari sebuah segitiga siku-siku. Jadi soal yang biasa kalian temui adalah ketika kita diminta untuk mencari panjang dari salah satu sisi yang dimiliki oleh segitiga siku-siku.
Artikel ini akan memaparkan penjelasan mengenai teorema pythagoras secara rinci.
Sejarah Teorema Pythagoras
Teorema Pythagoras pertama kali ditemukan oleh seorang filsuf dan matematikawan asal Yunani bernama Pythagoras. Namun, rumus teorema pythagoras pertama kali digunakan sudah sejak 1900-1600 SM oleh masyarakat Cina dan Babylonia. Selain itu, pada tahun 800 dan 400 di kitab Baudhayana Sulba Sutra di India.
Alasan mengapa akhirnya nama pythagoras yang diabadikan sebagai nama teori tersebut karena Pythagoras lah yang berhasil membuktikan rumus ini secara matematis.
Materi Teorema Pythagoras
Seperti yang telah dijelaskan di awal artikel, rumus teorema pythagoras ini merupakan cara untuk menghitung sisi-sisi dari segitiga siku-siku, di mana segitiga siku-siku memiliki tiga sisi, yaitu sisi alas, sisi tinggi, dan sisi miring atau hipotenusa.
Sebelum masuk ke pembahasan lebih lanjut, bagi kalian yang belum mengetahui seperti apa bentuk segitiga siku-siku, berikut adalah gambarnya:

Teorema pythagoras berbunyi:
“Di dalam sebuah segitiga siku-siku diberlakukan kuadrat dari sisi miring sama dengan jumlah kuadrat dari sisi-sisi lainnya”.
Dengan demikian ketiga sisi segitiga siku-siku memiliki hubungan yang saling terikat.
Teorema ini memiliki dua sifat wajib yang dimiliki, yaitu hanya berlaku pada segitiga siku-siku serta harus diketahui minimal dua sisi lebih dulu untuk bisa menentukan sisi lainnya.
Sedangkan tujuan dari teori ini pada dasarnya untuk menentukan panjang dari salah satu sisi suatu segitiga siku-siku. Adapun untuk sebuah segitiga siku-siku sebenarnya sangat mudah karena salah satu karakteristik dari segitiga siku-siku adalah memiliki salah satu sudut 90o.
Namun, teori ini juga bisa digunakan untuk menghitung panjang diagonal dari sebuah persegi atau balok dan kubus yang bentuknya juga seperti segitiga siku-siku.
Untuk pengembangannya teori ini juga bisa digunakan dalam kehidupan sehari-hari seperti misalnya untuk membuat wahana flying fox, perosotan, dan bahkan jalan tanjakan.
Rumus Teorema Pythagoras
Seperti yang telah dipaparkan di atas, bunyi dari teorema pythagoras menyebutkan bahwa sebuah segitiga siku-siku dengan penanda a,b,c, maka sisi kemiringannya (hipotenusa) sama dengan jumlah kuadrat dari sisi lainnya. Misalnya, sebuah segitiga memiliki alas a dan tinggi b, maka sisi kemiringannya adalah c. Artinya, jumlah kuadrat dari sisi c sama dengan jumlah kuadrat dari sisi a dan b.
Berdasarkan bunyi dari teorinya, berikut ini adalah cara untuk menghitung segitiga siku-siku dengan rumus teorema pythagoras:

Sesuai dengan gambar segitiga di atas maka rumusnya adalah:
Mencari sisi kemiringan:
c2 = a2 + b2
Mencari sisi alas:
b2 = c2 – a2
Mencari sisi tinggi atau samping:
a2 = c2 – b2
atau dapat diartikan bahwa a sisi tinggi, b sisi alas, dan c sisi miring.
Namun, sebenarnya ada cara lain untuk menentukan sisi dari segitiga siku-siku. Yaitu dengan menghafalkan triple pythagoras. Sebab, triple phytagoras ini adalah ukuran pasti dari sisi-sisi segitiga phytagoras. Berikut ini adalah angka-angka yang disebut dengan triple phytagoras:
- 3,4,5
- 5,12,13
- 6,8,10
- 7,24,25
- 8,15, 17
- 9, 12,15
- 10, 24, 26
- Dan seterusnya
Lantas apa maksud dari deret angka tersebut? Artinya adalah jika segitiga siku-siku memiliki tinggi 3 cm dan alas sepanjang 4 cm, maka sudah bisa dipastikan bahwa sisi kemiringan sepanjang 5 cm.
Dengan menghafalkan deret dari triple pythagoras itu tentunya akan mempermudah dan mempersingkat waktu ketika kita sedang mengerjakan sebuah soal pilihan ganda yang tidak perlu menuliskan langkah-langkah pengerjaan.
Contoh Soal Teorema Pythagoras
1. Segitiga siku-siku memiliki tinggi 9 cm dengan alas sepanjang 12 cm. Tentukanlah sisi kemiringan dari segitiga siku-siku tersebut.Jawab:
a = 9 cm
b = 12 cm
c = ?
c2 = a2 + b2
c2 = 92 + 122
c2= 81 + 144
c= √255
c = 15
Maka sisi miringnya adalah 15 cm.
2. Suatu segitiga siku-siku memiliki sisi kemiringan sepanjang 13 cm dan alas sepanjang 12 cm. Tentukanlah berapa tinggi dari segitiga siku-siku tersebut.
Jawab:
b = 12 cm
c = 13 cm
a = ?
a2 = c2 – b2
a2 = 132 - 122
a2 = 169 – 144
a2 = 25
a = √25
a = 5
Maka tinggi dari segitiga tersebut adalah 5 cm.
3. Segitiga siku-siku memiliki sisi hipotenusa 10 cm dan memiliki tinggi 6 cm. Berapakah panjang dari alas segitiga siku-siku tersebut.
Jawab:
a = 6 cm
c = 10 cm
b = ?
b2 = c2 – a2
b2 = 102 – 62
b2 = 100 – 36
b2 = 64
b = √64
b = 8
Maka panjang dari alas segitiga siku-siku tersebut adalah 8 cm.
4. Sebuah persegi panjang memiliki panjang 10 cm dan lebar 24 cm. Tentukanlah berapa panjang diagonal dari persegi panjang tersebut.
Jawab:
Jika digambarkan maka bentuk dari persegi panjang itu seperti ini:
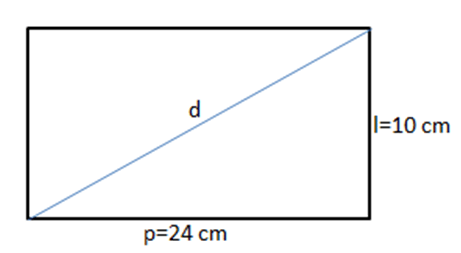
Dengan gambar persegi di atas maka dapat diartikan bahwa lebar dari persegi panjang itu sama dengan alas sebuah segitiga siku-siku yang dalam hal ini berarti 24 cm. Sedangkan panjang dari persegi panjang itu sama dengan tinggi dari segitiga siku-siku. Lantas berapakah panjang diagonal atau sisi miring dari persegi panjang tersebut?
a = 10 cm
b = 24 cm
c = ?
c2 = a2 + b2
c2 = 102 + 242
c2= 100 + 576
c= √676
c = 26
Maka panjang diagonal dari persegi panjang tersebut adalah 26 cm.
5. Pak Budi berencana untuk membuat wahana perosotan untuk anaknya dengan menggunakan peralatan yang ada di rumahnya. Jika jarak tempat tujuan akhir perosotan dengan tempat untuk naik yang tersedia di rumah adalah 8 meter dan tinggi dari tempat naik atau tangga dari perosotan itu adalah 6 meter, berapakah panjang sisi miring tempat untuk perosotan itu?
Jawab
Jika digambarkan dalam bentuk segitiga siku-siku maka bentuk dari flying fox itu adalah seperti ini:
Maka dapat diartikan bahwa tangga naik sama dengan tinggi segitiga, yaitu 6 cm dan jarak sama dengan alas, yaitu 8 cm.
a = 6 cm
b = 8 cm
c = ?
c
2 = a2 + b2
c2 = 62 + 82
c2= 36 + 64
c= √100
c = 10
Maka panjang dari sisi miring perosotan itu adalah 10 m.
Demikian adalah pembahasan mengenai materi rumus teorema pythagoras beserta contoh soalnya. Dengan metode STEAM, Sampoerna Academy mempersiapkan siswa dengan landasan global dan kualifikasi akademik yang diakui secara internasional.
Sampoerna Academy juga mendorong budaya inovasi dan kolaborasi. Selain itu, integrasi komunikasi, kecakapan atas berbagai macam bahasa, dan kolaborasi dalam kerja tim membuat berbeda dari kebanyakan sekolah lain di Asia Tenggara.
Source : wikihow.com - Tehorema Pythagoras


.webp)